NumPy: Eigenvalues & Eigenvectors

In this tutorial, we will explore NumPy's numpy.linalg.eig() function to deduce the eigenvalues and normalized eigenvectors of a square matrix.

Let $A$ be a square matrix.

In Linear Algebra, a scalar $\lambda$ is called an eigenvalue of matrix $A$ if there exists a column vector $v$ such that

$$ Av = \lambda v $$

and $v$ is non-zero. Any vector satisfying the above relation is known as eigenvector of the matrix $A$ corresponding to the eigen value $\lambda$.

We take an example matrix from a Schaum's Outline Series book Linear Algebra (4^th Ed.) by Seymour Lipschutz and Marc Lipson¹.

Given the matrix

$$ A = \begin{bmatrix} 3 & 1 \\ 2 & 2 \end{bmatrix}, $$

the column vector

$$ v = \begin{bmatrix} 1 \\ -2 \end{bmatrix} $$

is its eigenvector corresponding to the eigenvalue $\lambda = 1$ as

$$ Av = \begin{bmatrix} 3 & 1 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} 1 \\ -2 \end{bmatrix} = \begin{bmatrix} 1 \\ -2 \end{bmatrix} = 1v $$

Also,

$$ u = \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$

is its another eigenvector corresponding to the eigenvalue $\lambda = 4$ as

$$ Au = \begin{bmatrix} 3 & 1 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 4 \end{bmatrix} = 4 \begin{bmatrix} 1 \\ 1 \end{bmatrix} = 4u $$

NumPy has the numpy.linalg.eig() function to deduce the eigenvalues and normalized eigenvectors of a given square matrix. And since the returned eigenvectors are normalized, if you take the norm of the returned column vector, its norm will be 1.

So, take the cue from here. Since the returned eigenvectors are NORMALIZED, they may not always be the same eigenvectors as in the texts you are referring.

Note the two variables w and v assigned to the output of numpy.linalg.eig(). The first variable w is assigned an array of computed eigenvalues and the second variable v is assigned the matrix whose columns are the normalized eigenvectors corresponding to the eigenvalues in that order.

				
				import numpy as np
				a = np.array([[3, 1], [2, 2]])
				w, v = np.linalg.eig(a)
				print(w)
				print(v)
				
			

Executing the above Python script, the output is as follows:

Here we will explain the output. The first printed array is w, which constitutes the eigenvalues. The second printed matrix below it is v, whose columns are the eigenvectors corresponding to the eigenvalues in w. Meaning, to the w[i] eigenvalue, the corresponding eigenvector is the v[:,i] column in matrix v.

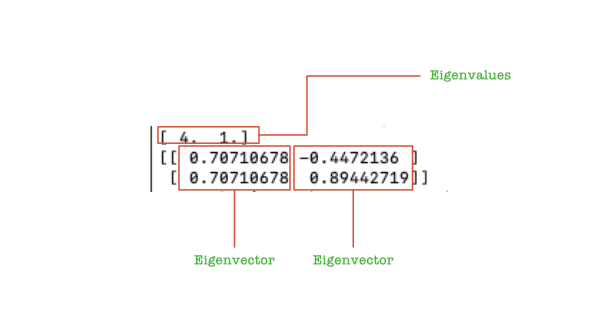
In NumPy, the ith column vector of a matrix v is extracted as

				
				v[:,i]
				
			

So, the eigenvalue

• w[0] goes with v[:,0]
• w[1] goes with v[:,1]

We will now check if the condition

$$ Av = \lambda v $$

holds here.

The LHS of the above equation $Av$ here is

				
				np.dot(a,v[:,0])
				
			

and the RHS part $\lambda v$ is

				
				np.dot(w[0],v[:,0])
				
			

So if the returned eigenvalues and eigenvectors are correct, the following line of script should return True

				
				print(np.allclose(np.dot(a,v[:,0]),np.dot(w[0],v[:,0])))
				
			

Also, just to see if the returned eigenvectors are normalized, use the numpy.linalg.norm() function to cross-check them. The below script should return 1.0 in both the print() statements.

				
				print(np.linalg.norm(v[:,0]))
				print(np.linalg.norm(v[:,1]))